คณิตพื้นฐาน เรื่อง การคูณ: ผลคูณของลำดับ

ถ้าพจน์แต่ละพจน์ของผลคูณไม่ได้เขียนออกมาทั้งหมด เราอาจจะใช้เครื่องหมายจุดไข่ปลาแทนพจน์ที่หายไป เช่นเดียวกับการดำเนินการอื่นๆ (เช่น การบวก) เช่น ผลคูณของจำนวนธรรมชาติ ตั้งแต่ 1-100 อาจเขียน $1 \cdot 2 \cdot \ldots \cdot 99 \cdot 100$ . และสามารถเขียนให้เครื่องหมายจุดไข่ปลาอยู่บริเวณกึ่งกลางแนวตั้งของแถวได้อีกด้วย คือ $1 \cdot 2 \cdot \cdots \cdot 99 \cdot 100$ .
นอกจากนี้แล้ว ผลคูณยังสามารถเขียนได้ด้วยเครื่องหมายผลคูณ ซึ่งมาจาก อักษร Π (Pi) ตัวใหญ่ ในอักษรกรีก. ตัวอย่างเช่น

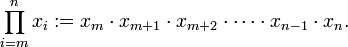
$\prod_{i=m}^{n} x_{i} := x_{m} \cdot x_{m+1} \cdot x_{m+2} \cdot \cdots \cdot x_{n-1} \cdot x_{n}.$

ตัวห้อยของประโยคสัญลักษณ์ข้างต้นแทนตัวแปรหุ่น (สำหรับประโยคนี้คือ $i$ ) และขอบเขตล่าง ( $m$ ); ตัวยกแทนขอบเขตบน ( $n$ ) เช่น

$\prod_{i=2}^{6} \left(1 + {1\over i}\right) = \left(1 + {1\over 2}\right) \cdot \left(1 + {1\over 3}\right) \cdot \left(1 + {1\over 4}\right) \cdot \left(1 + {1\over 5}\right) \cdot \left(1 + {1\over 6}\right) = {7\over 2}.$

เรายังสามารถหาผลคูณที่มีพจน์เป็นอนันต์ได้อีกด้วย เรียกว่าผลคูณอนันต์ ในการเขียน เราจะแทนที่ n ด้านบนด้วยเครื่องหมายอนันต์ (∞). ผลคูณของพจน์จะกำหนดด้วยขีดจำกัดของผลคูณของ $n$ พจน์แรก โดย $n$ เพิ่มขึ้นโดยไม่มีขอบเขต เช่น

$\prod_{i=m}^{\infty} x_{i} := \lim_{n\to\infty} \prod_{i=m}^{n} x_{i}$

นอกจากนี้ยังสามารถแทน $m$ ด้วยจำนวนลบอนันต์

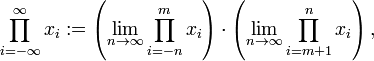
$\prod_{i=-\infty}^\infty x_i := \left(\lim_{n\to\infty}\prod_{i=-n}^m x_i\right) \cdot \left(\lim_{n\to\infty}\prod_{i=m+1}^n x_i\right),$

และสำหรับจำนวนเต็ม $m$ บางจำนวน สามารถกำหนดได้ทั้งอนันต์และลบอนันต์

เครดิต วิกีพีเดีย (สารานุกรมเสรี)

คณิตพื้นฐาน เรื่อง การคูณ

วันอังคารที่ 4 กันยายน พ.ศ. 2555

ผลคูณของลำดับ

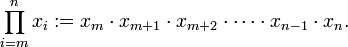
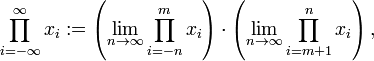
ไม่มีความคิดเห็น:

แสดงความคิดเห็น