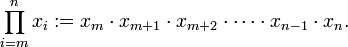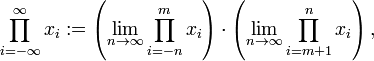คณิตพื้นฐาน เรื่อง การคูณ

วันอังคารที่ 4 กันยายน พ.ศ. 2555

การคูณเลขฐาน

                                                == 1. การคูณ ==
                                          1.1 การคูณเลขฐานสอง
ระบบเลขฐานสองมีตัวเลขเพียงสองตัวคือ 0 กับ 1
การคูณในระบบเลขฐานสอง เราสามารถกระทำได้ในลักษณะเช่นเดียวกับการคูณเลขฐานสิบ
ซึ่งก็คือ ทำการตั้งหลักของการคูณให้ตรงกัน โดยเริ่มจากบิท หรือหลักตัวเลขทางขวามือสุดก่อน
เมื่อได้ทำการคูณ ตัวตั้งด้วยตัวคูณทุกตำแหน่งแล้ว ก็ให้ทำการบวกโดยใช้กฎการบวกเลขฐานสองตามปกติทุกประการ
การคูณจึงมีหลักเกณฑ์ดังนี้
1 × 1 = 1
1 × 0 = 0
0 × 1 = 0
0 × 0 = 0
                                       1.2 การคูณเลขฐานแปด
ระบบเลขฐานแปดมีตัวเลขที่ใช้เพียงแปดตัวคือ 0 1 2 3 4 5 6 และ 7
การคูณในระบบเลขฐานแปด เราสามารถกระทำได้ในลักษณะเช่นเดียวกับการคูณเลขฐานสิบ
ซึ่งก็คือ ทำการตั้งหลักของการคูณให้ตรงกัน โดยเริ่มจากบิท หรือหลักตัวเลขทางขวามือสุดก่อน
แต่การคูณเลขฐานแปดนั้นมีหลักเกณฑ์สำคัญ คือ ถ้าผลลัพธ์ของการคูณเลขแต่ละบิทมีค่าเกิน 7
ให้นำ 8 ไปหารค่านั้น โดยนำผลลัพธ์ของการหารไปเป็นตัวทดในบิทถัดไป
และเศษของการหารใส่เป็นผลลัพธ์ในหลักที่ทำการคูณกันนั้น เมื่อได้ทำการคูณตัวตั้งด้วยตัวคูณทุกตำแหน่งแล้ว
ก็ให้ทำการบวกโดยใช้กฎการบวกเลขฐานแปดตามปกติทุกประการ
                                    1.3 การคูณเลขฐานสิบหก
ระบบเลขฐานสิบหกมีตัวเลขที่ใช้ 16 ตัวคือ 0 1 2 3 4 5 6 7 8 9 A B C D E และ F
การคูณในระบบเลขฐานสิบหก เราสามารถกระทำได้ในลักษณะเช่นเดียวกับการคูณเลขฐานสิบ
ซึ่งก็คือ ทำการตั้งหลักของการคูณให้ตรงกัน โดยเริ่มจากบิท หรือหลักตัวเลขทางขวามือสุดก่อน
แต่การคูณเลขฐานสิบหกนั้นมีหลักเกณฑ์สำคัญ คือ ถ้าผลลัพธ์ของการคูณเลขแต่ละบิทเมื่อคูณกันแล้วมีค่าเกิน 15 หรือค่า F
ให้นำ 16 ไปหารค่านั้น โดยนำผลลัพธ์ของการหารไปเป็นตัวทดในบิทถัดไป
และเศษของการหารใส่เป็นผลลัพธ์ในหลักที่ทำการคูณกันนั้น เมื่อได้ทำการคูณตัวตั้งด้วยตัวคูณทุกตำแหน่งแล้ว
ก็ให้ทำการบวกโดยใช้กฎการบวกเลขฐานสิบหกตามปกติทุกประการ
เครดิต วิกีพีเดีย (สารานุกรมเสรี)

ฟังก์ชันเชิงการคูณ

ในทฤษฎีจำนวน ฟังก์ชันเชิงการคูณ (อังกฤษ: multiplicative function) หมายถึงฟังก์ชันเลขคณิต f(n) สำหรับจำนวนเต็มบวก n ที่มีสมบัติดังนี้

f(1) = 1
f(ab) = f(a) f(b) เมื่อ a กับ b เป็นจำนวนเฉพาะสัมพัทธ์

นอกจากนี้ ถ้าฟังก์ชันเลขคณิต f(n) มีสมบัติทั้งสองข้อ สำหรับจำนวนเต็มบวก a, b ทุกจำนวนแม้ไม่ได้เป็นจำนวนเฉพาะสัมพัทธ์ ฟังก์ชันดังกล่าวจะเรียกว่า ฟังก์ชันเชิงการคูณบริบูรณ์ (completely multiplicative function, totally multiplicative function)

เครดิต วิกีพีเดีย (สารานุกรมเสรี)

ตัวผกผันการคูณ

ในทางคณิตศาสตร์ ตัวผกผันการคูณ (อินเวิร์สการคูณ) ของจำนวน x หมายถึงจำนวนที่คูณกับ x แล้วได้เอกลักษณ์การคูณ นั่นคือ 1 ตัวผกผันการคูณของ x เขียนแทนด้วย 1/x หรือ x⁻¹ และบางครั้งก็เรียกว่าส่วนกลับ (reciprocal) ของ x
เราสามารถคำนวณการตัวผกผันการคูณได้จากการหาร 1 ด้วยจำนวนที่ต้องการ ตัวอย่างเช่น ตัวผกผันการคูณของ 5 คือ 1/5 = 0.2 และส่วนกลับของ 0.25 คือ 1/0.25 = 4
0 เป็นจำนวนที่ไม่มีตัวผกผันการคูณ เนื่องจากจำนวนใดๆ คูณกับ 0 แล้วจะได้ 0 ซึ่งไม่ใช่ 1

เครดิต วิกีพีเดีย(สารานุกรมเสรี)

การคำนวณ

วิธีการคูณจำนวนโดยการทดลงกระดาษตามปกติ จำเป็นต้องใช้สูตรคูณที่ท่องจำ ซึ่งเป็นผลคูณของเลข 1−2 หลัก เพื่อให้สามารถตั้งคูณได้ แต่สำหรับวิธีการแบบชาวอียิปต์โบราณไม่เป็นเช่นนั้น ดังที่จะได้กล่าวต่อไป
การคูณจำนวนมากกว่าสองจำนวนบนเลขฐานสิบอาจทำให้เกิดความเบื่อหน่าย และก่อให้เกิดความผิดพลาดได้ง่าย จึงมีการคิดค้นลอการิทึมสามัญ (ลอการิทึมฐานสิบ) เพื่อทำให้คำนวณง่ายขึ้น นอกจากนั้นสไลด์รูลก็เป็นเครื่องมือช่วยคูณจำนวนอย่างรวดเร็ว และได้ผลลัพธ์ที่มีความแม่นยำประมาณสามหลัก และตั้งแต่ต้นคริสต์ศตวรรษที่ 20 ก็มีการประดิษฐ์เครื่องคิดเลขเชิงกล ซึ่งสามารถคูณเลขได้โดยอัตโนมัติถึง 10 หลัก ปัจจุบันนี้ใช้เครื่องคิดเลขอิเล็กทรอนิกส์และคอมพิวเตอร์แทน ซึ่งสามารถช่วยประหยัดเวลาการคูณเลขไปได้อย่างมาก

ขั้นตอนวิธีในประวัติศาสตร์

วิธีการคูณหลายวิธีมีการบันทึกไว้เป็นลายลักษณ์อักษรโดยอารยธรรมอียิปต์ กรีซ บาบิโลเนีย ลุ่มแม่น้ำสินธุ และจีน

อียิปต์

ดูบทความหลักที่ การคูณแบบอียิปต์โบราณ

วิธีการคูณจำนวนเต็มและเศษส่วนของชาวอียิปต์โบราณ ดังเช่นที่ระบุไว้ใน Ahmes Papyrus เป็นการบวกต่อเนื่องกันและการเพิ่มค่าเป็นสองเท่า ตัวอย่างเช่น การหาผลคูณของ 13 กับ 21 ก่อนอื่นจะต้องเพิ่มค่า 21 เป็นสองเท่า 3 ครั้ง ซึ่งจะได้ 1 × 21 = 21, 2 × 21 = 42, 4 × 21 = 84, 8 × 21 = 168 จากนั้นจึงรวมพจน์ที่เหมาะสมเข้าด้วยกันจนได้ผลคูณ นั่นคือ
13 × 21 = (1 + 4 + 8) × 21 = (1 × 21) + (4 × 21) + (8 × 21) = 21 + 84 + 168 = 273

บาลิโลเนีย

เนื่องจากชาวบาบิโลนใช้ระบบเลขเชิงตำแหน่ง ฐานหกสิบ ซึ่งเทียบได้กับเลขฐานสิบของปัจจุบัน แต่มีสัญลักษณ์แทนเลขโดดในแต่ละหลักถึง 60 ตัว ดังนั้นการคูณของชาวบาบิโลนจึงคล้ายกับวิธีการตั้งคูณในปัจจุบัน แต่เนื่องจากเป็นการยากที่จะจดจำผลคูณที่แตกต่างกันทั้งหมด 60 × 60 จำนวน นักคณิตศาสตร์ชาวบาบิโลนจึงใช้ตารางการคูณ (สูตรคูณ) เข้าช่วย ตารางเหล่านี้ประกอบด้วยรายชื่อของพหุคูณ 20 จำนวนแรกของจำนวนที่สำคัญ n ซึ่งจะได้ n, 2n, ..., 20n ตามด้วยพหุคูณของ 10n นั่นคือ 30n, 40n, และ 50n การคำนวณผลคูณคือการบวกค่าในตารางผลคูณเข้าด้วยกัน เช่น 53n ก็หาได้จากการบวกค่าของ 50n กับ 3n เป็นต้น

จีน

ในตำราเรียนคณิตศาสตร์ของจีนชื่อว่า Zhou Pei Suan Ching (周髀算經) เมื่อ 300 ปีก่อนคริสตกาล และหนังสือ The Nine Chapters on the Mathematical Art (九章算術) ได้อธิบายวิธีการคูณโดยการเขียนเป็นตัวหนังสือ ถึงแม้ว่านักคณิตศาสตร์ชาวจีนสมัยก่อนจะใช้ลูกคิดคำนวณด้วยมือทั้งการบวกและการคูณ

ลุ่มแม่น้ำสินธุ

นักคณิตศาสตร์ชาวฮินดูในอารยธรรมลุ่มแม่น้ำสินธุในสมัยก่อน ใช้กลวิธีที่หลากหลายเพื่อคำนวณการคูณ ซึ่งการคำนวณส่วนใหญ่จะทำบนกระดานชนวนขนาดเล็ก เทคนิคหนึ่งที่ใช้กันคือการคูณแลตทิซ (lattice multiplication) เริ่มตั้งแต่การวาดตารางขึ้นมาหนึ่งตาราง กำกับด้วยตัวตั้งและตัวคูณลงบนแถวและหลัก แต่ละช่องจะถูกแบ่งออกเป็นสองส่วนตามแนวทะแยง เป็นแลตทิซรูปสามเหลี่ยม ซึ่งเฉียงเป็นแนวเดียวกันทุกช่อง จากนั้นแต่ละช่องสี่เหลี่ยมให้เขียนผลคูณของเลขโดดที่กำกับไว้ลงไป ผลคูณของจำนวนจะหาได้จากการรวมแถวที่เป็นแนวเฉียงเข้าด้วยกันทีละหลัก

เครดิต วิกีพีเดีย (สารานุกรมเสรี)

นิยาม

สำหรับความหมายของการคูณ ผลคูณของจำนวนธรรมชาติ n และ m ใดๆ

$mn := \sum_{k=1}^n m$

กล่าวสั้นๆ คือ 'บวก m เข้ากับตัวเอง n ตัว' สามารถเขียนได้ในลักษณะนี้เพื่อให้ชัดเจนมากขึ้น

m × n = m + m + m + ... + m

หมายถึงมีจำนวน 'm' n ตัวบวกกันนั่นเอง

5 × 2 = 2 + 2 + 2 + 2 + 2 = 10
2 × 5 = 5 + 5 = 10
4 × 3 = 3 + 3 + 3 + 3 = 12
m × 6 = m + m + m + m + m + m

โดยใช้นิยาม เราสามารถพิสูจน์สมบัติของการคูณได้โดยง่ายดาย โดยดูจากสองตัวอย่างข้างต้น เรามีสมบัติว่า จำนวนสองจำนวนที่คูณกันสามารถสลับที่กันได้โดยผลคูณยังคงเดิม เราเรียกสมบัตินี้ว่า สมบัติการสลับที่ และ สมบัตินี้เป็นจริงสำหรับจำนวน x และ y ใดๆ นั่นคือ

x · y = y · x.

นอกจากนี้ การคูณยังมีสมบัติการเปลี่ยนหมู่อีกด้วย ความหมายสำหรับจำนวน x,y และ z ใดๆ คือ

(x · y)z = x(y · z).

หมายเหตุจากพีชคณิต: เครื่องหมายวงเล็บ หมายถึง การดำเนินภายในวงเล็บจะต้องกระทำก่อนการดำเนินการภายนอกวงเล็บ
การคูณมีสมบัติการแจกแจง เพราะ

x(y + z) = xy + xz.

มีสิ่งที่น่าสนใจเกี่ยวกับการคูณกับ 1 นั่นคือ

1 · x = x.

เราเรียก 1 ว่า จำนวนเอกลักษณ์
สำหรับเลข 0 เราจะได้

m · 0 = m + m + m +...+ m

เมื่อเรานำ '0' m ตัวมาบวกกัน ผลลัพธ์ที่ได้ย่อมเป็นศูนย์ นั่นคือ

m · 0 = 0

ไม่ว่า m จะเป็นจำนวนใด (แม้กระทั่งอนันต์).
การคูณกับจำนวนลบอาจจะต้องมีการคิดเล็กน้อย เริ่มจากการคูณ (−1) กับจำนวนเต็ม m ใดๆ

(−1)m = (−1) + (−1) +...+ (−1) = −m

นี่เป็นความจริงที่น่าสนใจว่า จำนวนลบ คือ จำนวนลบหนึ่ง คูณกับจำนวนบวกนั่นเอง เพราะฉะนั้นผลคูณระหว่างจำนวนบวกกับจำนวนลบทำได้โดยการคูณปกติ แล้วคูณด้วย (−1)

(−1)(−1) = −(−1) = 1

ในขณะนี้ เราสามารถสรุปการคูณระหว่างจำนวนเต็มสองจำนวนใดๆ ได้แล้ว และนิยามนี้ยังขยายไปสำหรับเซตของเศษส่วน หรือ จำนวนตรรกยะ และขยายไปถึงจำนวนจริงและจำนวนเชิงซ้อน
หลายคนอาจสงสัยถ้าบอกว่า ผลคูณของ'ไร้จำนวน' คือ 1
รูปแบบนิยามเรียกซ้ำของการคูณเป็นไปตามกฎ

x · 0 = 0

x · y = x + x·(y − 1)

เมื่อ x เป็นจำนวนจริง และ y เป็นจำนวนธรรมชาติ เมื่อเรากำหนดนิยามของการคูณจำนวนธรรมชาติแล้ว เรายังขยายผลไปถึงจำนวนเต็ม จำนวนจริง และจำนวนเชิงซ้อนได้

เครดิต วิกีพีเดีย (สารานุกรมเสรี)

ผลคูณของลำดับ

ถ้าพจน์แต่ละพจน์ของผลคูณไม่ได้เขียนออกมาทั้งหมด เราอาจจะใช้เครื่องหมายจุดไข่ปลาแทนพจน์ที่หายไป เช่นเดียวกับการดำเนินการอื่นๆ (เช่น การบวก) เช่น ผลคูณของจำนวนธรรมชาติ ตั้งแต่ 1-100 อาจเขียน $1 \cdot 2 \cdot \ldots \cdot 99 \cdot 100$ . และสามารถเขียนให้เครื่องหมายจุดไข่ปลาอยู่บริเวณกึ่งกลางแนวตั้งของแถวได้อีกด้วย คือ $1 \cdot 2 \cdot \cdots \cdot 99 \cdot 100$ .
นอกจากนี้แล้ว ผลคูณยังสามารถเขียนได้ด้วยเครื่องหมายผลคูณ ซึ่งมาจาก อักษร Π (Pi) ตัวใหญ่ ในอักษรกรีก. ตัวอย่างเช่น

$\prod_{i=m}^{n} x_{i} := x_{m} \cdot x_{m+1} \cdot x_{m+2} \cdot \cdots \cdot x_{n-1} \cdot x_{n}.$

ตัวห้อยของประโยคสัญลักษณ์ข้างต้นแทนตัวแปรหุ่น (สำหรับประโยคนี้คือ $i$ ) และขอบเขตล่าง ( $m$ ); ตัวยกแทนขอบเขตบน ( $n$ ) เช่น

$\prod_{i=2}^{6} \left(1 + {1\over i}\right) = \left(1 + {1\over 2}\right) \cdot \left(1 + {1\over 3}\right) \cdot \left(1 + {1\over 4}\right) \cdot \left(1 + {1\over 5}\right) \cdot \left(1 + {1\over 6}\right) = {7\over 2}.$

เรายังสามารถหาผลคูณที่มีพจน์เป็นอนันต์ได้อีกด้วย เรียกว่าผลคูณอนันต์ ในการเขียน เราจะแทนที่ n ด้านบนด้วยเครื่องหมายอนันต์ (∞). ผลคูณของพจน์จะกำหนดด้วยขีดจำกัดของผลคูณของ $n$ พจน์แรก โดย $n$ เพิ่มขึ้นโดยไม่มีขอบเขต เช่น

$\prod_{i=m}^{\infty} x_{i} := \lim_{n\to\infty} \prod_{i=m}^{n} x_{i}$

นอกจากนี้ยังสามารถแทน $m$ ด้วยจำนวนลบอนันต์

$\prod_{i=-\infty}^\infty x_i := \left(\lim_{n\to\infty}\prod_{i=-n}^m x_i\right) \cdot \left(\lim_{n\to\infty}\prod_{i=m+1}^n x_i\right),$

และสำหรับจำนวนเต็ม $m$ บางจำนวน สามารถกำหนดได้ทั้งอนันต์และลบอนันต์

เครดิต วิกีพีเดีย (สารานุกรมเสรี)

สัญกรณ์และคำศัพท์เฉพาะทาง

โดยทั่วไปการคูณสามารถเขียนโดยใช้เครื่องหมายคูณ (×) ระหว่างจำนวนทั้งสอง (ในรูปแบบสัญกรณ์เติมกลาง) ตัวอย่างเช่น

$2 \times 3 = 6$ (อ่านว่า 2 คูณ 3 เท่ากับ 6)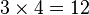

$3 \times 4 = 12$

$2 \times 3 \times 5 = 6 \times 5 = 30$

$2 \times 2 \times 2 \times 2 \times 2 = 32$

อย่างไรก็ตามก็ยังมีการใช้สัญกรณ์อื่นๆ แทนการคูณโดยทั่วไป อาทิ

ใช้จุดกลาง (·) หรือไม่ก็มหัพภาค (.) อย่างใดอย่างหนึ่ง เช่น 5 · 2 หรือ 5 . 2 การใช้จุดกลางเป็นมาตรฐานในสหรัฐอเมริกา สหราชอาณาจักร และประเทศอื่นๆ ที่ใช้มหัพภาคเป็นจุดทศนิยม แต่ในบางประเทศที่ใช้จุลภาคเป็นจุดทศนิยม จะใช้มหัพภาคเป็นการคูณแทน
ใช้ดอกจัน (*) เช่น 5*2 มักใช้ในภาษาโปรแกรมเพราะเครื่องหมายนี้ปรากฏอยู่บนทุกแป้นพิมพ์ และสามารถดูได้ง่ายบนจอมอนิเตอร์รุ่นเก่า การใช้เครื่องหมายนี้แทนการคูณเริ่มมีขึ้นตั้งแต่ภาษาฟอร์แทรน
ในพีชคณิต การคูณที่เกี่ยวกับตัวแปรมักจะเขียนให้อยู่ติดกัน เรียกว่า juxtaposition ตัวอย่างเช่น xy หมายถึง x คูณ y และ 5x หมายถึง 5 คูณ x เป็นต้น สัญกรณ์เช่นนี้สามารถใช้กับจำนวนที่ครอบด้วยวงเล็บ เช่น $5(2)$ หรือ $(5)(2)$ ก็จะหมายถึง 5 คูณ 2
ในการคูณเมทริกซ์ มีความแตกต่างระหว่างการใช้สัญลักษณ์กากบาทกับจุด กากบาทใช้แทนการคูณเวกเตอร์ ในขณะที่จุดใช้แทนการคูณสเกลาร์ ดังนั้นการตั้งชื่อเรียกจึงแตกต่างกันคือผลคูณไขว้และผลคูณจุดตามลำดับ

จำนวนที่ถูกคูณโดยทั่วไปเรียกว่า ตัวประกอบ (factor) หรือ ตัวตั้งคูณ (multiplicand) ส่วนจำนวนที่นำมาคูณเรียกว่า ตัวคูณ (multiplier) ตัวคูณของตัวแปรหรือนิพจน์ในพีชคณิตจะเรียกว่า สัมประสิทธิ์ (coefficient) ซึ่งจะเขียนไว้ทางซ้ายของตัวแปรหรือนิพจน์ เช่น 3 เป็นสัมประสิทธิ์ของ 3xy²
ผลลัพธ์ที่เกิดจากการคูณเรียกว่า ผลคูณ (product) หรือเรียกว่า พหุคูณ (multiple) ของตัวประกอบแต่ละตัวที่เป็นจำนวนเต็ม ตัวอย่างเช่น 15 คือผลคูณของ 3 กับ 5 และในขณะเดียวกัน 15 ก็เป็นทั้งพหุคูณของ 3 และพหุคูณของ 5 ด้วย

เครดิต วิกีพีเดีย (สารานุกรมเสรี)